50年后光孤子的光明前景

   

Andrea Blanco-Redondo, C. Martijn de Sterke, Chris Xu, Stefan Wabnitz and Sergei K. Turitsyn，The bright prospects of optical solitons after 50 years. Nature Photonics 17(10): 937–942 (2023).    

       Hasegawa和Tappert在1973年4月12日提交的一篇论文中提出了光纤中时间孤子的概念，意指通过二氧化硅的强度相关折射率（克尔效应）补偿色散引起的脉冲时间展宽。当时，运行在800 nm附近的第一代光纤传输系统尚未问世，光纤损耗徘徊在20 dBkm⁻¹左右，是当今光纤链路的100倍。然而，作者做出了一个引人注目的前瞻性预测：“如果吸收很小且非线性项可以与色散项相当”——这意味着1 ps脉冲的峰值功率为1 W——“可以预期脉冲形状的显著改变”，因为脉冲可以光孤子的形式不变地传播无限距离。早前，Zakharov和Shabat发现，光纤和非线性科学的关键数学模型之一，即非线性薛定谔方程，可以使用强大的逆散射变换方法进行积分，他们发现了该方程的解析单孤子和多孤子解。有等离子体物理学背景的Hasegawa，了解到类自聚焦背景下孤子的存在。这使他做出了富有想象力和鼓舞人心的预测，即在未来的某一天，孤子可以以万亿比特的速率在全球传输信息。现在，简要介绍了这一预测是如何演变的，目的不是全面回顾该领域，而是简要说明几十年来光学时间孤子研究如何与其他技术突破相结合而发生的变化。

       1980年，Mollenauer、Stolen和Gordon首次在1.55 μm处观测到光纤中的孤子。除了基阶孤子态的无扰动传播外，他们还报道了在更高功率下对高阶孤子动力学的观测，引入了孤子的一个新应用，即非线性光脉冲压缩（压缩因子约为3.5）。三年后，Mollenauer及其同事证明了13阶孤子的压缩因子约为27，将7 ps脉冲转换为260 fs脉冲。到20世纪80年代末，通过高阶孤子压缩实现了少周期脉冲。

       在首次证实时间孤子十年后，人们意识到，如果光孤子被周期性放大，它们可以在功率的周期性损耗-增益变化中幸存下来，并在超长距离上传输，使路径平均传播近似等于无损传播。从Hasegawa和Tappert向前看20年：1.55 μm附近的第三个窗口中的光纤损耗现在降低到0.2 dBkm⁻¹。这与掺铒光纤放大器的发明相结合，实际上消除了对传输距离的损耗限制。然后，重点是减轻掺铒光纤放大器引入的光噪声。噪声会随机干扰孤子：特别是，基阶孤子的频率和到达时间受到Gordon–Haus时间抖动的影响。利用色散补偿光纤抑制时间抖动的研究导致了色散管理孤子的实验发现和理论描述。贝尔实验室的孤子先驱Linn Mollenauer和Pavel Mamyshev评估了通过结合波分复用器、掺铒光纤放大器和色散管理孤子在跨洋距离上传输大量数据的潜力。

       在21世纪之交，当Nick Doran领导的Marconi Solstis团队在澳大利亚安装了一个基于色散管理孤子技术的5745公里长的地面光纤系统时，光孤子的概念成为了商业现实。然而，在21世纪初，用于超长距离波分复
用传输的移相键控和相干通信的引入，使得能够通过数字数据处理以及机器学习技术对传输损伤进行电子补偿，极大地降低了对开关键控调制解决方案的商业兴趣，包括基于孤子的通信系统。

       然而，最初的光孤子概念通过扩展到新的应用而得到了扩展和加强，例如，超连续产生、频率梳和锁模光纤激光器，其中孤子和色散管理孤子由光噪声自发形成，这是自然界中自组织的一个令人印象深刻的例子。事实上，正是在超短脉冲激光器的背景下，光孤子在过去20年中找到了无可争议的领域：通过将孤子概念扩展到耗散系统，实现了这一方向的飞跃，在耗散系统中，非线性不仅平衡了色散且增益平衡了线性和非线性损耗机制，从而将孤子理论扩展到路径平均增益-损耗动力学之外。事实上，耗散孤子代表了非线性光学腔的真实时空本征模；因此，它们有望用于许多新兴的光子技术和应用。图1展示了已经出现和新兴的孤子技术和应用的例子以及一些目前研究的新孤子概念。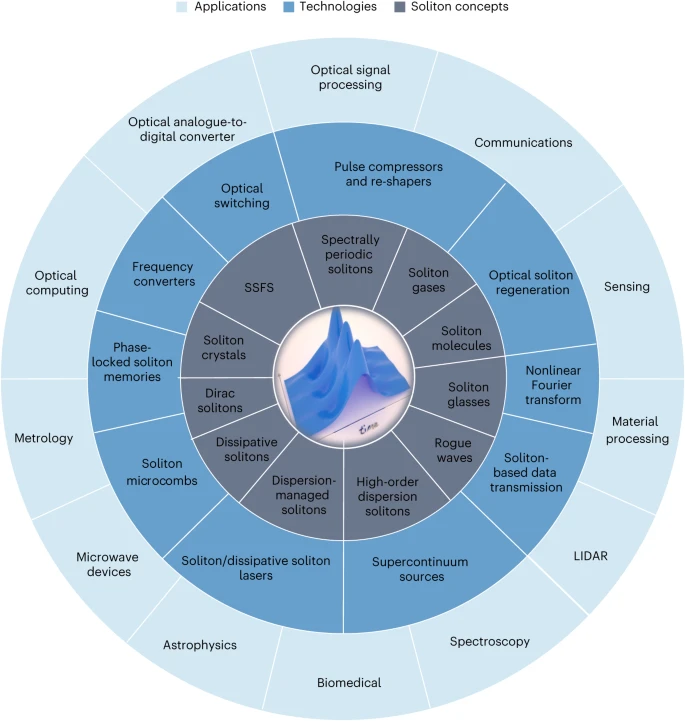

                       图1 孤子概念、技术与应用。孤子理论概念、技术以及当前和潜在的未来应用领域的例子。

孤子在超快激光技术中的未来

       解决孤子激光器能量限制的另一种研究途径是使用大模场面积或空心光纤来降低非线性。孤子能量与波导的非线性参数y=2πn2/入Aef成反比，其中，n2是材料非线性系数，入是波长，Aef是有效模场面积。通过增加有效模场面积Aef或降低材料非线性系数n2,在高阶模光纤、光子晶体棒和空心光子带隙光纤中，孤子能量可以放大几个数量级。反谐振空心光纤和大芯空心毛细管光纤中产生的孤子可以分别达到微焦和毫焦以上的水平。除此之外，这些光纤的使用使高阶孤子压缩成为亚周期脉冲。 

      通过增加光纤直径来扩大光纤激光器脉冲能量的方法自然会产生多模光纤孤子激光器。孤子的美妙之处在于，正如Hasegawa在1980年富有远见的论文中再次预测的那样，它们不仅可以在多模光纤中存活，甚至可以通过克尔非线性来补偿色散与模式色散。在空分复用通信对多模光纤重新产生兴趣的刺激下，Renninger和Wise花了长达33年的时间才通过实验观察到多模光纤孤子。光纤激光器不同横模的非线性诱导锁定为全锁模或时空锁模带来了一个实用的平台，这使锁模激光器的脉冲能量相对于单模激光器增加几个数量级。这是多模光纤的一个显著特性，因为在体介质中，多维非线性薛定谔方程具有自聚焦、波坍缩和不稳定孤子的特点。

       可以预计，基于孤子技术，如耗散孤子、超连续谱生成和孤子自频移，将在脉冲激光系统的进一步发展中发挥重要作用，无论是在单模光纤还是多模光纤中，将光发射扩展到新的光谱波段（例如中红外区域），并通过机器学习方法增强对激光发射的控制。
 

孤子在微腔频率梳中的未来

关于利用高阶色散来提高性能的趋势，有人认为，基于四阶色散环构建孤子克尔微梳可以实现平坦的光谱，从而降低频率线之间的变化，获得更宽的带宽，甚至提高泵浦至梳的转换效率。尽管仅基于高偶阶色散的孤子克尔微腔尚未在实验上实现，但已有具有前景的设计表明，该领域可能注定会改变已建立的孤子微梳界结构。
 

孤子在生物医学应用中的未来

       波导孤子和孤子自频移提供的灵活性和便利性已经在生物医学成像中得到了应用，如多光子显微镜和相干拉曼散射成像，这些成像依赖于短脉冲激光器。尽管基于孤子的飞秒光源和孤子自频移的优点得到了广泛认可（例如，紧凑和低成本等），但这些光源大多用于研究型实验室，其中许多已用于概念验证，而不是常规应用。尽管成本高昂，但直到今天，多光子成像的主力仍然是体锁模激光器和最近开发的高重复率（几兆赫）非共线式光参量放大器。为了使基于孤子和孤子自频移的系统具有广泛的生物医学应用，未来基于孤子的系统的性能必须匹配或超过锁模激光器和非共线式光参量放大器所提供的性能。例如，商用非共线式光参量放大器可以在约1300 nm和约1700 nm的多光子成像的长波长光谱窗口内常规产生微焦级的波长可调谐飞秒脉冲。这种性能还没有被基于孤子和孤子自频移的系统所匹配。在1300 nm左右的波长下，由于负色散的要求，产生高能、波长可调谐的孤子更具挑战性。最近开发的反谐振空心光纤具有大的传输带和易于定制的色散特性。当由光纤振荡器或光纤啁啾脉冲放大系统在1060 nm附近泵浦时，这种光纤中的孤子产生和孤子自频移有可能在约1300 nm处获得比非共线式光参量放大器更好的性能，例如，脉冲能量为1–10 μJ，1300 nm附近的宽波长可调谐性和兆赫兹脉冲重复率。因此，它们可以成为非共线式光参量放大器系统的低成本替代品。波导孤子和孤子自频移为飞秒光源提供了一个紧凑、低成本和鲁棒的方便平台。这种平台在波长可调谐锁模激光器无宽带增益介质存在的波长区域中将特别有吸引力。随着对非线性波传播的理解不断加深以及波导设计和制造方面的创新，孤子系统有望在大量生物医学领域应用。

孤子在电信和信号处理中的未来

       使用孤子进行信息传输的最初想法是基于使用具有直接检测的归零、开关键控调制格式，这足以满足20世纪90年代的光网络传输能力。本世纪初，实用相干检测通信系统的发展使人们能够过渡到使用光学相位编码的多级调制格式，这导致了更高的光谱效率。在相干系统中，与Nyquist型载波脉冲相比，基阶光孤子通过非线性平衡色散的能力不如有限的孤子光谱效率重要。相比之下，在接收器处对振幅和相位的检测开启了特征值通信的可能性，正如Hasegawa和Nyu所提出的，这再次基于非线性薛定谔方程的可积性。逆散射变换法（也称为非线性傅立叶变换）可以通过电子后处理精确补偿色散和非线性传输损伤，并为非线性光纤信道引入了全新的调制格式，包括多孤子信号编码和调制。

新兴的光孤子概念及有关的新科学正揭开面纱

       使用具有不同自然或工程非线性和/或色散的新材料，孤子出现了新的前景。更高阶非线性、更通用的色散类型，包括纯四阶色散及其高阶变体、布拉格型结构和其他工程介质，可以产生新型孤子和不同的应用。人们几乎没有触及表面——毫无疑问，还有许多其他有趣的非线性类型和色散关系，可以产生具有新颖性质的孤子。

       光孤子的一个迷人的机会在于多维系统。特别是，对高度多模光学系统和孤子的研究是一个新兴的令人兴奋的研究领域：多模孤子代表了时空光弹概念的离散（在空间域）版本，尽管到目前为止，由于其固有的坍缩趋势，这一点一直难以理解。由于渐变折射率光纤中具有引导性的抛物线折射率分布，多模孤子可以传播数万个色散长度。它们的传播伴随着时空周期振荡，这导致高强度色散光谱边带发射到中红外区域。从基本角度来看，多模孤子的理论描述将需要将弱湍流或热力学方法扩展到强非线性区域，包括时间维度，这仍然是一个悬而未决的问题。

        总之，光孤子的科学和应用有着丰富而卓越的历史，也有着光明的前景。色散效应和非线性效应之间以及增益和损耗之间的相互作用，在多维系统中，可能会给物理学家和数学家带来有趣的问题，而光孤子对扰动的鲁棒性预计对许多工程应用仍然极具吸引力。孤子理论为掌握非线性动力学铺平了道路，为新技术和设备提供了平台，为新材料和结构的工程设定了目标，从而汇集了光子学的三个主要驱动因素：材料科学、光学工程和新科学概念。